
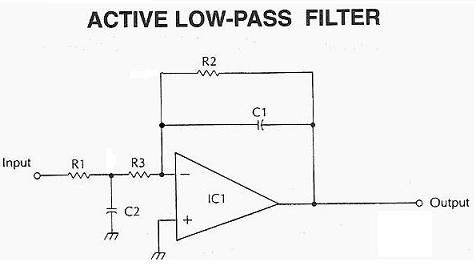
You can do the same with any Spice-based simulator like the free LT-Spice. I did the simulation for you with Labcenter Electronics Proteus. Simply because 2 3.33 = 10, and 3.33 × 6 = 20.) That means that, above its cut-off frequency, its attenuation is increased by 6 dB each time the frequency is doubled, or by 20 dB each time it is multiplied by 10. This filter is called a first-order filter, and it provides an attenuation of 6 dB per octave or 20 dB per decade. The capacitor impedance gets lower when the frequency increases, and the signal power is attenuated. The basic low-pass filter is built with one series resistor and one capacitor to ground (see Figure 3). I propose to start with the most basic designs: RC filters. If you decide that you need a filter with 0.01 dB of ripple up to 10 kHz and 100 dB of rejection from 11 kHz upward, you will probably need plenty of time and cash for the design. Of course, these specifications must be established with care. Lastly, you will very probably want to specify that the filter must provide a given minimum attenuation, called rejection, above some frequency f SB. The maximum tolerated variation of signal power in the pass-band (here from DC to f PB) is called the ripple of the filter. For example, a 50- or 60-Hz notch filter is included in virtually every weight scale to remove EMC perturbations from the surrounding power lines.Ī filter (low-pass in this case) is specified by its cutoff frequency f3dB, its ripple in the pass-band, and its rejection in the stopband.īut perhaps an attenuation of 3 dB is already too much for your application. Lastly, a band stop filter, often called a notch filter, does the opposite, and it attenuates a selected range of frequencies. For example, any radio frequency receiver is a band-pass filter, providing attenuation of all signals except for frequencies close to its preset frequency. Band-pass filters are a combination of both, and they attenuate all frequencies below or above a given range. Conversely, a high-pass filter attenuates the low frequencies, and could in particular remove any DC component of a signal. It is perfect for removing high-frequency noise on a signal coming from a sensor. A low-pass filter lets the low frequencies pass through, but attenuates high-frequency signals. Figure 1 depicts the most classic filter types. By definition, a filter is a circuit that attenuates some signals more than others, depending on their frequency. I promise, no Laplace transforms or poles or zeros, just electronics. I will try to help you to specify a filter, understand the main filter variants, and efficiently use some great computer-aided design tools. My goal for this article is more pragmatic. I bet a textbook about filters full of math would bore you, right? Well, relax. Filters are definitively useful, simple, and even fun. Unfortunately, filter design, or even their use, is often perceived as a difficult task close to black magic. So analog filters must be in the bag of tricks of any designer. This month, I’ll focus on filters-more precisely, analog frequency-selective filters, which are used in audio devices, as well as for noise reduction, antialiasing before digitizing a signal, separation of frequency-multiplexed signals, frequency response correction, and so on. Op-amps shine in plenty of applications-in particular, to build active filters. I spoke about operational amplifiers (op-amps) in my last few columns.


 0 kommentar(er)
0 kommentar(er)
